مریم میرزایی
مریم میرزاخانی نخستین دختری بود که در المپیاد ریاضی ایران طلا گرفت. وی نخستین کسی بود که دو سال
مدال طلا گرفت و نخستین دانشآموز شرکتکننده از ایران بود که در آزمون المپیاد ریاضی نمره کامل
گرفت. به محض اینکه [میرزاخانی] در هاروارد شروع کرد، مشخص بود که کارش خوب است. مشخص بود که تز
دکترایش یک تز انقلابی است
ریاضیات یونانی
مقدمه:
ریاضیات یونانی بسیار پیچیدهتر از ریاضیات مورد استفاده توسط فرهنگ قبل آغاز شده بود، میباشد. تمام
مساتندات از ریاضیات پیش یونانی، نشان دادن استفاده از استدلال قیاسی با مشاهدات مورد استفاده برای ایجاد
قوانین کلی میباشد. ریاضیدانان یونانی، در مقابل استفاده استدلال استقرایی یا قیاسی، از منطق برای استنتاج
نتایج از تعاریف و اصول موضوعه استفاده میکردند.
اثباتی از کتاب اصول اقلیدس (حدود ۳۰۰ پیش از میلاد)، این کتاب را به طور گسترده به عنوان مؤثرترین کتاب
درسی تمام زمانها بر میشمرند.
تالس یکی ریاضیدانانی است که برای نخستین بار به وسیله استدلال منطقی و بدون استفاده از شهود، چند قضیه مهم
هندسه را ثابت کرد. فیثاغورس (یا به عبارت درستتر فیثاغورسیان که پیروان و شاگردان او بودند) نیز سهم
بسزایی در تکامل ریاضیات برهانی داشت. خلاصهای از کارهای فیثاغورسیان را مرور میکنیم: این گروه نخستین
گامها را در رشد نظریه اعداد برداشتند، مانند معرفی اعداد متحابه، تام، ناقص و زاید و نیز معرفی اعداد مصور
مثلثی، مربعی، مخمسی (مراجعه کنید به صفحه ۷۲ تا ۷۴ جلد اول کتاب تاریخ ریاضیات هاوارد د. ایوز) . (ب)
نخستین برهان منطقی و درست از قضیه فیثاغورس که بابلیان قدیم بدون برهان از آن استفاده میکردند. (ج) کشف
عدد گنگ که یکی از حوادث مهم تاریخ ریاضیات است. (د) ابداع جبر هندسی برای بیان اتحادهای جبری در قالب
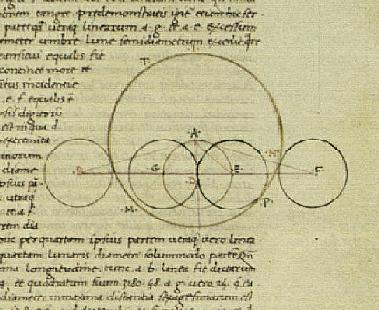
اصطلاحات هندسی. برای توضیح بیشتر، اتحاد را به این وسیله با شکل زیر «ثابت» میکنیم: (ه) حل هندسی معادلات
درجه دوم. برای نمونه با فرض اینکه a و b دو عدد مثبت باشند، طول x را چنان به دست میآوریم که x جواب
معادله باشد. این کار را در شکل زیر انجام دادهایم. (با این کار میتوان برای هر عدد طبیعی n، را رسم کرد.
کافیست دایرهای به قطر n+۱ رسم کنیم) .
ریاضیات در یونان باستان
در قرن ششم پیش از میلاد، که آغاز پیشرفتهای علمی یونان بود، نام تالس، به عنوان اولین ریاضیدان یونانی به
چشم میخورد. وی در سفر به مصر مقداری قضایا و علم هندسه را یاد گرفت. وی بعضی اصول و قضایای هندسی را کشف
کرده و در طرحریزی علم ریاضی سهیم است. اثبات این قضایا را به او نسبت میدهند:
۱. قطر دایره را به دو قسمت مساوی تقسیم میکند ۲. زوایای طرفین قاعده مثلث متساوی الساقین با یکدیگر برابرند
۳. چون دو خط مستقیم یکدیگر را قطع کنند، زوایای متقابل با یکدیگر برابر است ۴. زاویه محاط بر نصف دایره
قائمه است ۵. اظلاع دو مثلث متشابه با یکدیگر تناسب دارند ۶. چون دو زاویه و ضلع بین آنها از دو مثلث با
یکدیگر متساوی باشند آن دو مثلث قابل انطباقاند.
دومین عالم سرشناس ریاضی در یونان که پس از تالس آمد، فیثاغورس است. او از شاگردان تالس بود و از دستاوردهای
او در ریاضی میتوان به اعداد مثلث، مجموعه زوایای داخلی هر مثلث و اثبات آن اشاره کرد. دموکریتوس ابدرایی
نیز از جمله ریاضیدانان مشهور آن زمان بود که درباره تماس دایره با کره، اعداد، هندسه، مقادیر اصم و چند
مورد دیگر به کشفهای بزرگی دست یافت.
نام دیگری در علم ریاضیات که به آن بسیار اشاره میشود، نام بقراط (هیپوکراتس) است که برخی او را همان بقراط
حکیم میدانند و گروهی دیگر معتقدند که او فردی جداگانه است که با این حکیم، معاصر بوده است. به هر روی، در
زمان او سه مسأله بزرگ ریاضی مطرح بود: ۱. تربیع دایره ۲. تضعیف مکعب ۳. تثلیث زاویه. بقراط روی دو مسأله
اول کار کرد و با وجود اینکه موفق به حل کامل آنها نشد، ولی راه حلهای بسیار سودمندی به جا گذاشت.
افلاطون نیز به نوبه خود در پیشبرد علم ریاضی یونان بسیار مؤثر بود. او در آکادمیای که برای آموزش جوانان
بر پا کرده بود، روی آموزش ریاضیات تأکید بسیاری میکرد و حتی بر سر در آکادمیاشنوشته شده بود: ( (هرکس
ریاضی نمیداند، وارد نشود) ) . شاگرد او ارسطو نیز با وجود اینکه بیشتر به عنوان یک فلسفهدان و پزشک
شناخته میشود، در ریاضیات هم دستی داشت و میان بدیهیات با اصول موضوعه تفاوت گذاشت؛ مثل قانون نفی حد واسط
و قانون تناقض.
اسامی بسیار دیگری را میتوان در علم ریاضیات یونان باستان برشمرد. از زنون الئایی گرفته تا اوقلیدس مگارائی
و بروسون هراکلئایی و تئودوروس کورنه ئی. هر کدام از این افراد به نوعی در پیشبرد ریاضیات یونان سهیم
بودهاند ولی از نام بردن همه آنها خودداری کرده و به ذکر همین چند مورد که احتمالاً مهمترینها محسوب
میشوند، اکتفا میکنیم.